我的位置：主页 > K12教育 > 物理 > 可微一定可导吗

可微一定可导吗

来源：快懂网 2021-07-17 17:21 6743 人看过

不一定。如果是一元函数，那么可微一定可导，而且可导也一定可微，也就是说在一元函数中，可微和可导是等价的。如果是多元函数，那么可微一定可导，但是可导不一定可微，也就是说在某

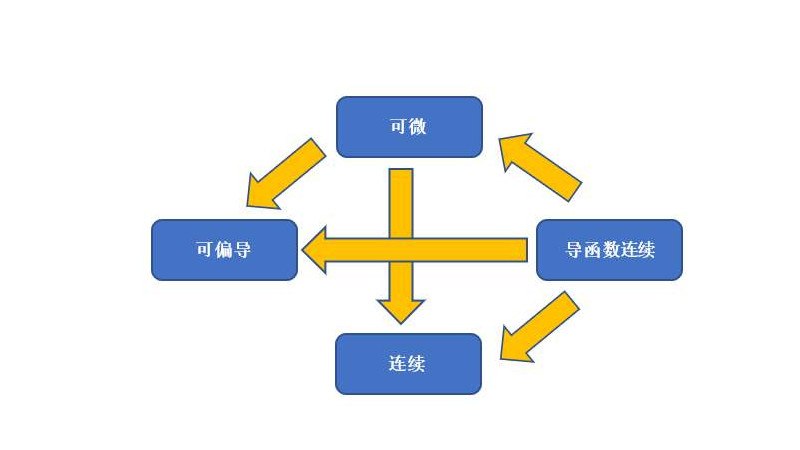
在学习函数的过程中，常常涉及到可微、可导的问题，如果函数在某点可以微分的话，那么函数在这个点就必连续。如果函数在该点连续，而且左导数右导数都存在且相等，这是函数可导的充要条件，那么可微一定可导吗？可微不一定可导。如果是一元函数，那么可微一定可导，而且可导也一定可微，也就是说在一元函数中，可微和可导是等价的。如果是多元函数，那么可微一定可导，但是可导不一定可微，也就是说在某一点可以求偏导，但并不一定可以推出在这一点可微。

推荐文章：实对称矩阵的特征向量一定正交吗沿着电场线方向电势一定降低吗 ph大于7一定是碱性溶液吗

延伸阅读：: 实对称矩阵的特征向量一定正交吗; 沿着电场线方向电势一定降低吗; ph大于7一定是碱性溶液吗

免责声明：本站所提供的内容均来源于网友提供或网络搜集，由本站编辑整理，仅供个人研究、交流学习使用。如涉及版权问题，请联系本站管理员予以更改或删除。

给作者点赞，鼓励TA抓紧创作！

有用 6743

更多精彩内容，请关注快懂生活微信公众号

更多物理相关知识

实对称矩阵的特征向量一定正交吗

2021-07-173885 人看过

实对称矩阵的特征向量不一定会正交。假设n*n阶单位矩阵为实对称矩阵，并且任何n维向量都是
沿着电场线方向电势一定降低吗

2021-07-173935 人看过

沿着电场线方向电势不一定是降低的。某点电荷可分为正负两种，当沿着电场线方向移动是正
ph大于7一定是碱性溶液吗

2021-07-177695 人看过

PH大于7的溶液实际上并不一定就是碱性溶液。因为ph还是跟温度有一些联系的。例如在温度升高
二阶可导和二阶连续可导的区别

2021-07-17962 人看过

二阶可导和二阶连续可导，在函数方面都有二阶导数，但是对于函数二阶可导，二阶导数的连
曲线运动一定是什么运动

2021-07-178844 人看过

一定是变速运动，变速运动指的是在运动过程中速度发生了变化。同时速度是一个矢量，既有
溶质一定是固体吗

2021-07-173809 人看过

溶质并不一定就是固体溶质，可能是固体，也可能是液体，甚至是气体。当然固体的溶质是存
固体的密度一定比液体的密度大吗

2021-07-176465 人看过

不一定会比液体的密度更大一些，这种说法属于不正确的，大多数固体的密度要比液体的更大